kNN Implementation
Original source code provided by Stanford University, see course notes for cs231n: Convolutional Neural Networks for Visual Recognition.
# -*- coding: utf-8 -*-
"""
Created on Sun Sep 22 11:13:47 2019
@author: abbottjc
"""
import os
import random
import numpy as np
from cs231n.data_utils import load_CIFAR10
import matplotlib.pyplot as plt
# This is a bit of magic to make matplotlib figures appear inline in the notebook
# rather than in a new window.
%matplotlib inline
plt.rcParams['figure.figsize'] = (10.0, 8.0) # set default size of plots
plt.rcParams['image.interpolation'] = 'nearest'
plt.rcParams['image.cmap'] = 'gray'
# Some more magic so that the notebook will reload external python modules;
# see http://stackoverflow.com/questions/1907993/autoreload-of-modules-in-ipython
%load_ext autoreload
%autoreload 2
# Set cifar10 path directory
cifar10_dir = r'datasets\cifar-10-batches-py'
# Make sure data hasn't already been loaded
try:
del X_train, y_train
del X_test, y_test
print("Data previously loaded... removing data")
except:
pass
X_train, y_train, X_test, y_test = load_CIFAR10(cifar10_dir)
# As a sanity check, we print out the size of the training and test data.
print('Training data shape: ', X_train.shape)
print('Training labels shape: ', y_train.shape)
print('Test data shape: ', X_test.shape)
print('Test labels shape: ', y_test.shape)
Training data shape: (50000, 32, 32, 3)
Training labels shape: (50000,)
Test data shape: (10000, 32, 32, 3)
Test labels shape: (10000,)
# Visualize some examples from the dataset.
# We show a few examples of training images from each class.
classes = ['plane', 'car', 'bird', 'cat', 'deer', 'dog', 'frog', 'horse', 'ship', 'truck']
num_classes = len(classes)
samples_per_class = 7
for y, cls in enumerate(classes):
idxs = np.flatnonzero(y_train == y)
idxs = np.random.choice(idxs, samples_per_class, replace=False)
for i, idx in enumerate(idxs):
plt_idx = i * num_classes + y + 1
plt.subplot(samples_per_class, num_classes, plt_idx)
plt.imshow(X_train[idx].astype('uint8'))
plt.axis('off')
if i == 0:
plt.title(cls)
plt.show()

# Subsample the data for more efficient code execution in this exercise
# Subsample the training set to 5000 images
num_training = 5000
mask = list(range(num_training))
X_train = X_train[mask]
y_train = y_train[mask]
# Subsample the test data set to 500 images
num_test = 500
mask = list(range(num_test))
X_test = X_test[mask]
y_test = y_test[mask]
# Reshape the image data into rows
X_train = np.reshape(X_train, (X_train.shape[0], -1))
X_test = np.reshape(X_test, (X_test.shape[0], -1))
print(X_train.shape, X_test.shape)
(5000, 3072) (500, 3072)
from cs231n.classifiers import KNearestNeighbor
# Create a kNN classifier instance.
# Remember that training a kNN classifier is a noop:
# the Classifier simply remembers the data and does no further processing
classifier = KNearestNeighbor()
classifier.train(X_train, y_train)
# Compute_distances_two_loops.
# Test implementation:
dists = classifier.compute_distances_two_loops(X_test)
print(dists.shape)
Calculating.....
Complete
(500, 5000)
# We can visualize the distance matrix: each row is a single test example and
# its distances to training examples
plt.imshow(dists, interpolation='none')
plt.show()

# Now implement the function predict_labels and run the code below:
# We use k = 1 (which is Nearest Neighbor).
y_test_pred = classifier.predict_labels(dists, k=1)
# Compute and print the fraction of correctly predicted examples
num_correct = np.sum(y_test_pred == y_test)
accuracy = float(num_correct) / num_test
print('Got %d / %d correct => accuracy: %f' % (num_correct, num_test, accuracy))
Got 137 / 500 correct => accuracy: 0.274000
y_test_pred = classifier.predict_labels(dists, k=5)
num_correct = np.sum(y_test_pred == y_test)
accuracy = float(num_correct) / num_test
print('Got %d / %d correct => accuracy: %f' % (num_correct, num_test, accuracy))
Got 139 / 500 correct => accuracy: 0.278000
dists_one = classifier.compute_distances_one_loop(X_test)
# Make sure that the vectorized implementation is correct. Make sure that it
# agrees with the two-loop implementation.
difference = np.linalg.norm(dists - dists_one, ord='fro')
print('One loop difference was: %f' % (difference, ))
if difference < 0.001:
print('Good! The distance matrices are the same')
else:
print('Uh-oh! The distance matrices are different')
computing...
One loop difference was: 0.000000
Good! The distance matrices are the same
# Implement the fully vectorized version inside compute_distances_no_loops
dists_two = classifier.compute_distances_no_loops(X_test)
# check that the distance matrix agrees with the one we computed before:
difference = np.linalg.norm(dists - dists_two, ord='fro')
print('No loop difference was: %f' % (difference, ))
if difference < 0.001:
print('Good! The distance matrices are the same')
else:
print('Uh-oh! The distance matrices are different')
No loop difference was: 0.000000
Good! The distance matrices are the same
# Compare how fast the implementations are
def time_function(f, *args):
"""
Call a function f with args and return the time (in seconds) that it took to execute.
"""
import time
tic = time.time()
f(*args)
toc = time.time()
return toc - tic
two_loop_time = time_function(classifier.compute_distances_two_loops, X_test)
print('Two loop version took %f seconds' % two_loop_time)
one_loop_time = time_function(classifier.compute_distances_one_loop, X_test)
print('One loop version took %f seconds' % one_loop_time)
no_loop_time = time_function(classifier.compute_distances_no_loops, X_test)
print('No loop version took %f seconds' % no_loop_time)
# You should see significantly faster performance with the fully vectorized implementation!
# NOTE: depending on what machine you're using,
# you might not see a speedup when you go from two loops to one loop,
# and might even see a slow-down.
Calculating.....
Complete
Two loop version took 25.233699 seconds
computing...
One loop version took 66.645878 seconds
No loop version took 0.335277 seconds
num_folds = 5
k_choices = [1, 3, 5, 8, 10, 12, 15, 20, 50, 100]
X_train_folds = []
y_train_folds = []
################################################################################
# Split up the training data into folds. After splitting, X_train_folds and #
# y_train_folds should each be lists of length num_folds, where #
# y_train_folds[i] is the label vector for the points in X_train_folds[i]. #
################################################################################
X_train_folds = np.array_split(X_train, num_folds)
Y_train_folds = np.array_split(y_train, num_folds)
# A dictionary holding the accuracies for different values of k that we find
# when running cross-validation. After running cross-validation,
# k_to_accuracies[k] should be a list of length num_folds giving the different
# accuracy values that we found when using that value of k.
k_to_accuracies = {}
################################################################################
# Perform k-fold cross validation to find the best value of k. For each #
# possible value of k, run the k-nearest-neighbor algorithm num_folds times, #
# where in each case you use all but one of the folds as training data and the #
# last fold as a validation set. Store the accuracies for all fold and all #
# values of k in the k_to_accuracies dictionary. #
################################################################################
for k in k_choices:
k_to_accuracies[k] = []
for k in k_choices:
for j in range(num_folds):
# Use all but one folds as our crossval training set
X_train_crossval = np.vstack(X_train_folds[0:j] + X_train_folds[j+1:])
# Use the last fold as our crossval test set
X_test_crossval = X_train_folds[j]
y_train_crossval = np.hstack(Y_train_folds[0:j]+Y_train_folds[j+1:])
y_test_crossval = Y_train_folds[j]
# Train the k-NN Classifier using the crossval training set
classifier.train(X_train_crossval, y_train_crossval)
# Use the trained classifer to compute the distance of our crossval test set
dists_crossval = classifier.compute_distances_no_loops(X_test_crossval)
y_test_pred = classifier.predict_labels(dists_crossval, k)
num_correct = np.sum(y_test_pred == y_test_crossval)
accuracy = float(num_correct) / num_test
k_to_accuracies[k].append(accuracy)
# Print out the computed accuracies
for k in sorted(k_to_accuracies):
for accuracy in k_to_accuracies[k]:
print('k = %d, accuracy = %f' % (k, accuracy))
k = 1, accuracy = 0.526000
k = 1, accuracy = 0.514000
k = 1, accuracy = 0.528000
k = 1, accuracy = 0.556000
k = 1, accuracy = 0.532000
k = 3, accuracy = 0.478000
k = 3, accuracy = 0.498000
k = 3, accuracy = 0.480000
k = 3, accuracy = 0.532000
k = 3, accuracy = 0.508000
k = 5, accuracy = 0.496000
k = 5, accuracy = 0.532000
k = 5, accuracy = 0.560000
k = 5, accuracy = 0.584000
k = 5, accuracy = 0.560000
k = 8, accuracy = 0.524000
k = 8, accuracy = 0.564000
k = 8, accuracy = 0.546000
k = 8, accuracy = 0.580000
k = 8, accuracy = 0.546000
k = 10, accuracy = 0.530000
k = 10, accuracy = 0.592000
k = 10, accuracy = 0.552000
k = 10, accuracy = 0.568000
k = 10, accuracy = 0.560000
k = 12, accuracy = 0.520000
k = 12, accuracy = 0.590000
k = 12, accuracy = 0.558000
k = 12, accuracy = 0.566000
k = 12, accuracy = 0.560000
k = 15, accuracy = 0.504000
k = 15, accuracy = 0.578000
k = 15, accuracy = 0.556000
k = 15, accuracy = 0.564000
k = 15, accuracy = 0.548000
k = 20, accuracy = 0.540000
k = 20, accuracy = 0.558000
k = 20, accuracy = 0.558000
k = 20, accuracy = 0.564000
k = 20, accuracy = 0.570000
k = 50, accuracy = 0.542000
k = 50, accuracy = 0.576000
k = 50, accuracy = 0.556000
k = 50, accuracy = 0.538000
k = 50, accuracy = 0.532000
k = 100, accuracy = 0.512000
k = 100, accuracy = 0.540000
k = 100, accuracy = 0.526000
k = 100, accuracy = 0.512000
k = 100, accuracy = 0.526000
# plot the raw observations
for k in k_choices:
accuracies = k_to_accuracies[k]
plt.scatter([k] * len(accuracies), accuracies)
# plot the trend line with error bars that correspond to standard deviation
accuracies_mean = np.array([np.mean(v) for k,v in sorted(k_to_accuracies.items())])
accuracies_std = np.array([np.std(v) for k,v in sorted(k_to_accuracies.items())])
plt.errorbar(k_choices, accuracies_mean, yerr=accuracies_std)
plt.title('Cross-validation on k')
plt.xlabel('k')
plt.ylabel('Cross-validation accuracy')
plt.show()
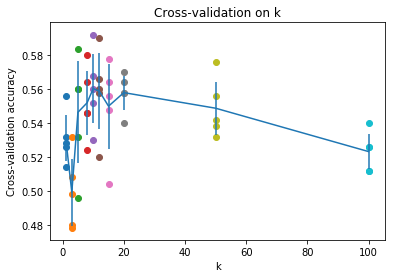
# Based on the cross-validation results above, choose the best value for k,
# retrain the classifier using all the training data, and test it on the test
# data. You should be able to get above 28% accuracy on the test data.
best_k = 10
classifier = KNearestNeighbor()
classifier.train(X_train, y_train)
y_test_pred = classifier.predict(X_test, k=best_k)
# Compute and display the accuracy
num_correct = np.sum(y_test_pred == y_test)
accuracy = float(num_correct) / num_test
print('Got %d / %d correct => accuracy: %f' % (num_correct, num_test, accuracy))
Got 141 / 500 correct => accuracy: 0.282000