Dropout

Original source code and content provided by Stanford University, see course notes for cs231n: Convolutional Neural Networks for Visual Recognition.

Dropout

Dropout [1] is a technique for regularizing neural networks by randomly setting some output activations to zero during the forward pass. In this exercise you will implement a dropout layer and modify your fully-connected network to optionally use dropout.

[1] Geoffrey E. Hinton et al, “Improving neural networks by preventing co-adaptation of feature detectors”, arXiv 2012

# As usual, a bit of setup
from __future__ import print_function
import time
import numpy as np
import matplotlib.pyplot as plt
from cs231n.classifiers.fc_net import *
from cs231n.data_utils import get_CIFAR10_data
from cs231n.gradient_check import eval_numerical_gradient, eval_numerical_gradient_array
from cs231n.solver import Solver

%matplotlib inline
plt.rcParams['figure.figsize'] = (10.0, 8.0) # set default size of plots
plt.rcParams['image.interpolation'] = 'nearest'
plt.rcParams['image.cmap'] = 'gray'

# for auto-reloading external modules
# see http://stackoverflow.com/questions/1907993/autoreload-of-modules-in-ipython
%load_ext autoreload
%autoreload 2

def rel_error(x, y):
  """ returns relative error """
  return np.max(np.abs(x - y) / (np.maximum(1e-8, np.abs(x) + np.abs(y))))

run the following from the cs231n directory and try again:
python setup.py build_ext --inplace
You may also need to restart your iPython kernel

# Load the (preprocessed) CIFAR10 data.

data = get_CIFAR10_data()
for k, v in data.items():
  print('%s: ' % k, v.shape)

X_train:  (49000, 3, 32, 32)
y_train:  (49000,)
X_val:  (1000, 3, 32, 32)
y_val:  (1000,)
X_test:  (1000, 3, 32, 32)
y_test:  (1000,)

Dropout forward pass

In the file cs231n/layers.py, implement the forward pass for dropout. Since dropout behaves differently during training and testing, make sure to implement the operation for both modes.

Once you have done so, run the cell below to test your implementation.

np.random.seed(231)
x = np.random.randn(500, 500) + 10

for p in [0.25, 0.4, 0.7]:
  out, _ = dropout_forward(x, {'mode': 'train', 'p': p})
  out_test, _ = dropout_forward(x, {'mode': 'test', 'p': p})

  print('Running tests with p = ', p)
  print('Mean of input: ', x.mean())
  print('Mean of train-time output: ', out.mean())
  print('Mean of test-time output: ', out_test.mean())
  print('Fraction of train-time output set to zero: ', (out == 0).mean())
  print('Fraction of test-time output set to zero: ', (out_test == 0).mean())
  print()

Running tests with p =  0.25
Mean of input:  10.000207878477502
Mean of train-time output:  10.014059116977283
Mean of test-time output:  9.984207926115783
Fraction of train-time output set to zero:  0.749784
Fraction of test-time output set to zero:  0.750336

Running tests with p =  0.4
Mean of input:  10.000207878477502
Mean of train-time output:  9.981867341626124
Mean of test-time output:  10.021655901377157
Fraction of train-time output set to zero:  0.600644
Fraction of test-time output set to zero:  0.599216

Running tests with p =  0.7
Mean of input:  10.000207878477502
Mean of train-time output:  9.988455973951861
Mean of test-time output:  9.996128027553349
Fraction of train-time output set to zero:  0.301024
Fraction of test-time output set to zero:  0.300136

Dropout backward pass

In the file cs231n/layers.py, implement the backward pass for dropout. After doing so, run the following cell to numerically gradient-check your implementation.

np.random.seed(231)
x = np.random.randn(10, 10) + 10
dout = np.random.randn(*x.shape)

dropout_param = {'mode': 'train', 'p': 0.2, 'seed': 123}
out, cache = dropout_forward(x, dropout_param)
dx = dropout_backward(dout, cache)
dx_num = eval_numerical_gradient_array(lambda xx: dropout_forward(xx, dropout_param)[0], x, dout)

# Error should be around e-10 or less
print('dx relative error: ', rel_error(dx, dx_num))

dx relative error:  5.44560814873387e-11

Fully-connected nets with Dropout

In the file cs231n/classifiers/fc_net.py, modify your implementation to use dropout. Specifically, if the constructor of the network receives a value that is not 1 for the dropout parameter, then the net should add a dropout layer immediately after every ReLU nonlinearity. After doing so, run the following to numerically gradient-check your implementation.

np.random.seed(231)
N, D, H1, H2, C = 2, 15, 20, 30, 10
X = np.random.randn(N, D)
y = np.random.randint(C, size=(N,))

for dropout in [1, 0.75, 0.5]:
  print('Running check with dropout = ', dropout)
  model = FullyConnectedNet([H1, H2], input_dim=D, num_classes=C,
                            weight_scale=5e-2, dtype=np.float64,
                            dropout=dropout, seed=123)

  loss, grads = model.loss(X, y)
  print('Initial loss: ', loss)
  
  # Relative errors should be around e-6 or less; Note that it's fine
  # if for dropout=1 you have W2 error be on the order of e-5.
  for name in sorted(grads):
    f = lambda _: model.loss(X, y)[0]
    grad_num = eval_numerical_gradient(f, model.params[name], verbose=False, h=1e-5)
    print('%s relative error: %.2e' % (name, rel_error(grad_num, grads[name])))
  print()

Running check with dropout =  1
Initial loss:  2.3004790897684924
W1 relative error: 1.48e-07
W2 relative error: 2.21e-05
W3 relative error: 3.53e-07
b1 relative error: 5.38e-09
b2 relative error: 2.09e-09
b3 relative error: 5.80e-11

Running check with dropout =  0.75
Initial loss:  2.302371489704412
W1 relative error: 1.90e-07
W2 relative error: 4.76e-06
W3 relative error: 2.60e-08
b1 relative error: 4.73e-09
b2 relative error: 1.82e-09
b3 relative error: 1.70e-10

Running check with dropout =  0.5
Initial loss:  2.3042759220785896
W1 relative error: 3.11e-07
W2 relative error: 1.84e-08
W3 relative error: 5.35e-08
b1 relative error: 2.58e-08
b2 relative error: 2.99e-09
b3 relative error: 1.13e-10

Regularization experiment

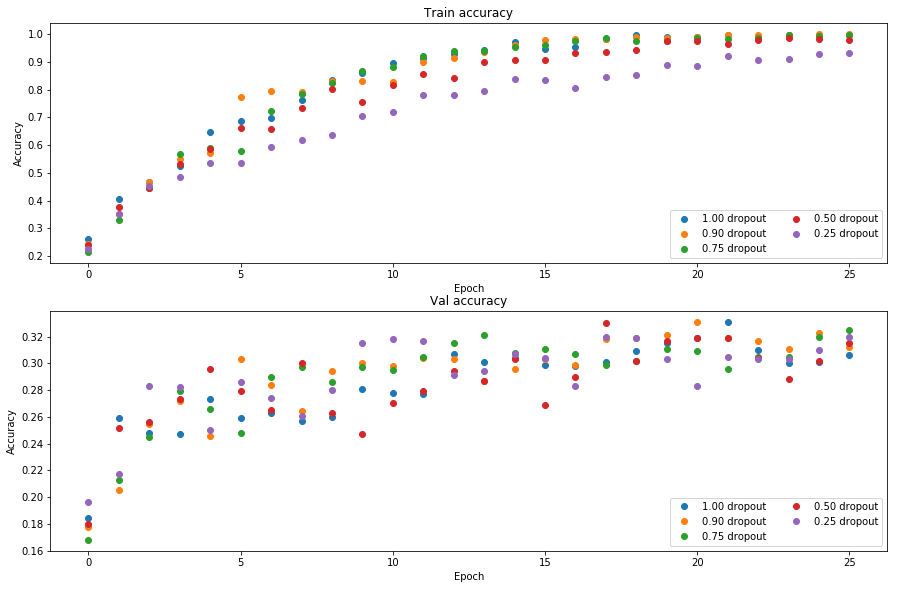
As an experiment, we will train a pair of two-layer networks on 500 training examples: one will use no dropout, and one will use a keep probability of 0.25. We will then visualize the training and validation accuracies of the two networks over time.

# Train two identical nets, one with dropout and one without
np.random.seed(231)
num_train = 500
small_data = {
  'X_train': data['X_train'][:num_train],
  'y_train': data['y_train'][:num_train],
  'X_val': data['X_val'],
  'y_val': data['y_val'],
}

solvers = {}
dropout_choices = [1, 0.9, 0.75, 0.5, 0.25]
for dropout in dropout_choices:
  model = FullyConnectedNet([500], dropout=dropout)
  print(dropout)

  solver = Solver(model, small_data,
                  num_epochs=25, batch_size=100,
                  update_rule='adam',
                  optim_config={
                    'learning_rate': 5e-4,
                  },
                  verbose=True, print_every=100)
  solver.train()
  solvers[dropout] = solver
  print()

1
(Iteration 1 / 125) loss: 7.856644
(Epoch 0 / 25) train acc: 0.260000; val_acc: 0.184000
(Epoch 1 / 25) train acc: 0.404000; val_acc: 0.259000
(Epoch 2 / 25) train acc: 0.468000; val_acc: 0.248000
(Epoch 3 / 25) train acc: 0.526000; val_acc: 0.247000
(Epoch 4 / 25) train acc: 0.646000; val_acc: 0.273000
(Epoch 5 / 25) train acc: 0.686000; val_acc: 0.259000
(Epoch 6 / 25) train acc: 0.698000; val_acc: 0.263000
(Epoch 7 / 25) train acc: 0.762000; val_acc: 0.257000
(Epoch 8 / 25) train acc: 0.836000; val_acc: 0.260000
(Epoch 9 / 25) train acc: 0.860000; val_acc: 0.281000
(Epoch 10 / 25) train acc: 0.894000; val_acc: 0.278000
(Epoch 11 / 25) train acc: 0.912000; val_acc: 0.277000
(Epoch 12 / 25) train acc: 0.928000; val_acc: 0.307000
(Epoch 13 / 25) train acc: 0.944000; val_acc: 0.301000
(Epoch 14 / 25) train acc: 0.970000; val_acc: 0.304000
(Epoch 15 / 25) train acc: 0.948000; val_acc: 0.299000
(Epoch 16 / 25) train acc: 0.952000; val_acc: 0.298000
(Epoch 17 / 25) train acc: 0.982000; val_acc: 0.301000
(Epoch 18 / 25) train acc: 0.996000; val_acc: 0.309000
(Epoch 19 / 25) train acc: 0.990000; val_acc: 0.315000
(Epoch 20 / 25) train acc: 0.988000; val_acc: 0.319000
(Iteration 101 / 125) loss: 0.336620
(Epoch 21 / 25) train acc: 0.996000; val_acc: 0.331000
(Epoch 22 / 25) train acc: 0.990000; val_acc: 0.310000
(Epoch 23 / 25) train acc: 0.996000; val_acc: 0.300000
(Epoch 24 / 25) train acc: 0.998000; val_acc: 0.301000
(Epoch 25 / 25) train acc: 0.996000; val_acc: 0.306000

0.9
(Iteration 1 / 125) loss: 10.861761
(Epoch 0 / 25) train acc: 0.244000; val_acc: 0.178000
(Epoch 1 / 25) train acc: 0.350000; val_acc: 0.205000
(Epoch 2 / 25) train acc: 0.466000; val_acc: 0.255000
(Epoch 3 / 25) train acc: 0.548000; val_acc: 0.272000
(Epoch 4 / 25) train acc: 0.572000; val_acc: 0.246000
(Epoch 5 / 25) train acc: 0.772000; val_acc: 0.303000
(Epoch 6 / 25) train acc: 0.796000; val_acc: 0.284000
(Epoch 7 / 25) train acc: 0.790000; val_acc: 0.264000
(Epoch 8 / 25) train acc: 0.832000; val_acc: 0.294000
(Epoch 9 / 25) train acc: 0.830000; val_acc: 0.300000
(Epoch 10 / 25) train acc: 0.828000; val_acc: 0.298000
(Epoch 11 / 25) train acc: 0.898000; val_acc: 0.304000
(Epoch 12 / 25) train acc: 0.912000; val_acc: 0.303000
(Epoch 13 / 25) train acc: 0.934000; val_acc: 0.287000
(Epoch 14 / 25) train acc: 0.962000; val_acc: 0.296000
(Epoch 15 / 25) train acc: 0.978000; val_acc: 0.303000
(Epoch 16 / 25) train acc: 0.984000; val_acc: 0.299000
(Epoch 17 / 25) train acc: 0.982000; val_acc: 0.318000
(Epoch 18 / 25) train acc: 0.988000; val_acc: 0.319000
(Epoch 19 / 25) train acc: 0.986000; val_acc: 0.321000
(Epoch 20 / 25) train acc: 0.990000; val_acc: 0.331000
(Iteration 101 / 125) loss: 0.018121
(Epoch 21 / 25) train acc: 0.996000; val_acc: 0.319000
(Epoch 22 / 25) train acc: 0.998000; val_acc: 0.317000
(Epoch 23 / 25) train acc: 0.998000; val_acc: 0.311000
(Epoch 24 / 25) train acc: 1.000000; val_acc: 0.323000
(Epoch 25 / 25) train acc: 1.000000; val_acc: 0.312000

0.75
(Iteration 1 / 125) loss: 11.589987
(Epoch 0 / 25) train acc: 0.214000; val_acc: 0.168000
(Epoch 1 / 25) train acc: 0.328000; val_acc: 0.213000
(Epoch 2 / 25) train acc: 0.444000; val_acc: 0.245000
(Epoch 3 / 25) train acc: 0.568000; val_acc: 0.279000
(Epoch 4 / 25) train acc: 0.590000; val_acc: 0.266000
(Epoch 5 / 25) train acc: 0.580000; val_acc: 0.248000
(Epoch 6 / 25) train acc: 0.724000; val_acc: 0.290000
(Epoch 7 / 25) train acc: 0.784000; val_acc: 0.297000
(Epoch 8 / 25) train acc: 0.822000; val_acc: 0.286000
(Epoch 9 / 25) train acc: 0.866000; val_acc: 0.297000
(Epoch 10 / 25) train acc: 0.882000; val_acc: 0.295000
(Epoch 11 / 25) train acc: 0.922000; val_acc: 0.305000
(Epoch 12 / 25) train acc: 0.940000; val_acc: 0.315000
(Epoch 13 / 25) train acc: 0.938000; val_acc: 0.321000
(Epoch 14 / 25) train acc: 0.952000; val_acc: 0.308000
(Epoch 15 / 25) train acc: 0.962000; val_acc: 0.311000
(Epoch 16 / 25) train acc: 0.974000; val_acc: 0.307000
(Epoch 17 / 25) train acc: 0.986000; val_acc: 0.299000
(Epoch 18 / 25) train acc: 0.976000; val_acc: 0.302000
(Epoch 19 / 25) train acc: 0.976000; val_acc: 0.311000
(Epoch 20 / 25) train acc: 0.986000; val_acc: 0.309000
(Iteration 101 / 125) loss: 0.720892
(Epoch 21 / 25) train acc: 0.984000; val_acc: 0.296000
(Epoch 22 / 25) train acc: 0.986000; val_acc: 0.305000
(Epoch 23 / 25) train acc: 0.998000; val_acc: 0.305000
(Epoch 24 / 25) train acc: 0.994000; val_acc: 0.320000
(Epoch 25 / 25) train acc: 0.998000; val_acc: 0.325000

0.5
(Iteration 1 / 125) loss: 13.793884
(Epoch 0 / 25) train acc: 0.238000; val_acc: 0.180000
(Epoch 1 / 25) train acc: 0.378000; val_acc: 0.252000
(Epoch 2 / 25) train acc: 0.444000; val_acc: 0.256000
(Epoch 3 / 25) train acc: 0.530000; val_acc: 0.273000
(Epoch 4 / 25) train acc: 0.584000; val_acc: 0.296000
(Epoch 5 / 25) train acc: 0.662000; val_acc: 0.279000
(Epoch 6 / 25) train acc: 0.658000; val_acc: 0.265000
(Epoch 7 / 25) train acc: 0.734000; val_acc: 0.300000
(Epoch 8 / 25) train acc: 0.802000; val_acc: 0.263000
(Epoch 9 / 25) train acc: 0.754000; val_acc: 0.247000
(Epoch 10 / 25) train acc: 0.818000; val_acc: 0.270000
(Epoch 11 / 25) train acc: 0.856000; val_acc: 0.279000
(Epoch 12 / 25) train acc: 0.842000; val_acc: 0.294000
(Epoch 13 / 25) train acc: 0.898000; val_acc: 0.287000
(Epoch 14 / 25) train acc: 0.906000; val_acc: 0.303000
(Epoch 15 / 25) train acc: 0.908000; val_acc: 0.269000
(Epoch 16 / 25) train acc: 0.932000; val_acc: 0.290000
(Epoch 17 / 25) train acc: 0.936000; val_acc: 0.330000
(Epoch 18 / 25) train acc: 0.944000; val_acc: 0.302000
(Epoch 19 / 25) train acc: 0.974000; val_acc: 0.317000
(Epoch 20 / 25) train acc: 0.976000; val_acc: 0.319000
(Iteration 101 / 125) loss: 1.915017
(Epoch 21 / 25) train acc: 0.966000; val_acc: 0.319000
(Epoch 22 / 25) train acc: 0.978000; val_acc: 0.304000
(Epoch 23 / 25) train acc: 0.986000; val_acc: 0.288000
(Epoch 24 / 25) train acc: 0.982000; val_acc: 0.302000
(Epoch 25 / 25) train acc: 0.980000; val_acc: 0.315000

0.25
(Iteration 1 / 125) loss: 18.316434
(Epoch 0 / 25) train acc: 0.226000; val_acc: 0.196000
(Epoch 1 / 25) train acc: 0.350000; val_acc: 0.217000
(Epoch 2 / 25) train acc: 0.454000; val_acc: 0.283000
(Epoch 3 / 25) train acc: 0.484000; val_acc: 0.282000
(Epoch 4 / 25) train acc: 0.534000; val_acc: 0.250000
(Epoch 5 / 25) train acc: 0.534000; val_acc: 0.286000
(Epoch 6 / 25) train acc: 0.592000; val_acc: 0.274000
(Epoch 7 / 25) train acc: 0.618000; val_acc: 0.261000
(Epoch 8 / 25) train acc: 0.638000; val_acc: 0.280000
(Epoch 9 / 25) train acc: 0.704000; val_acc: 0.315000
(Epoch 10 / 25) train acc: 0.720000; val_acc: 0.318000
(Epoch 11 / 25) train acc: 0.782000; val_acc: 0.317000
(Epoch 12 / 25) train acc: 0.782000; val_acc: 0.291000
(Epoch 13 / 25) train acc: 0.794000; val_acc: 0.294000
(Epoch 14 / 25) train acc: 0.838000; val_acc: 0.307000
(Epoch 15 / 25) train acc: 0.834000; val_acc: 0.304000
(Epoch 16 / 25) train acc: 0.806000; val_acc: 0.283000
(Epoch 17 / 25) train acc: 0.844000; val_acc: 0.320000
(Epoch 18 / 25) train acc: 0.852000; val_acc: 0.319000
(Epoch 19 / 25) train acc: 0.888000; val_acc: 0.303000
(Epoch 20 / 25) train acc: 0.884000; val_acc: 0.283000
(Iteration 101 / 125) loss: 10.936090
(Epoch 21 / 25) train acc: 0.920000; val_acc: 0.305000
(Epoch 22 / 25) train acc: 0.906000; val_acc: 0.303000
(Epoch 23 / 25) train acc: 0.910000; val_acc: 0.303000
(Epoch 24 / 25) train acc: 0.930000; val_acc: 0.310000
(Epoch 25 / 25) train acc: 0.932000; val_acc: 0.320000

# Plot train and validation accuracies of the two models

train_accs = []
val_accs = []
for dropout in dropout_choices:
  solver = solvers[dropout]
  train_accs.append(solver.train_acc_history[-1])
  val_accs.append(solver.val_acc_history[-1])

plt.subplot(3, 1, 1)
for dropout in dropout_choices:
  plt.plot(solvers[dropout].train_acc_history, 'o', label='%.2f dropout' % dropout)
plt.title('Train accuracy')
plt.xlabel('Epoch')
plt.ylabel('Accuracy')
plt.legend(ncol=2, loc='lower right')
  
plt.subplot(3, 1, 2)
for dropout in dropout_choices:
  plt.plot(solvers[dropout].val_acc_history, 'o', label='%.2f dropout' % dropout)
plt.title('Val accuracy')
plt.xlabel('Epoch')
plt.ylabel('Accuracy')
plt.legend(ncol=2, loc='lower right')

plt.gcf().set_size_inches(15, 15)
plt.show()